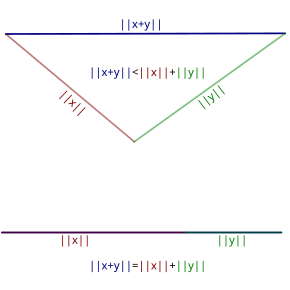
Dalam matematika , pertidaksamaan segitiga menyatakan bahwa untuk sebarang segitiga , jumlah panjang dua sisi haruslah lebih besar daripada panjang sisi yang lain. [ 1 ] [ 2 ]
Dalam geometri Euklides dan beberapa geometri lainnya ini adalah teorema . Dalam kasus Euklides, baik pada pernyataan lebih kecil atau sama dengan dan lebih besar atau sama dengan , kesamaan terjadi hanya jika segitiga memiliki sebuah sudut 180° dan dua sudut 0°, seperti yang ditunjukkan pada contoh bawah gambar di kanan. Ketidaksamaan tersebut dapat dilihat secara intuitif dalam R 2 atau R 3 . Gambar di kanan menunjukkan dua contohnya
Geometri Euklides
Euklides membuktikan pertidaksamaan segitiga pada geometri bidang datar menggunakan konstruksi pada gambar. [ 3 ] Dengan menggunakan sebarang segitiga ABC , sebuah segitiga sama kaki dibentuk dengan sisi BC , dan kaki lain BD yang terletak pada perpanjangan garis AB . Dengan menunjukkan bahwa sudut β > α , dapat disimpulkan AD > AC . Namun AD = AB + BD = AB + BC , sehingga didapatkan AB + BC > AC . Bukti ini muncul dalam buku Element Euklides, Buku 1, Proposisi 20. [ 4 ]
Daftar pustaka
- ^ Wolfram MathWorld - http://mathworld.wolfram.com/TriangleInequality.html
- ^ Khamsi, Mohamed A. (2001). An introduction to metric spaces and fixed point theory . W. A. Kirk. New York: John Wiley. ISBN 0-471-41825-0 . OCLC 45393989 .
- ^ Jacobs, Harold R. (2003). Geometry : seeing, doing, understanding (edisi ke-3rd ed). New York: W.H. Freeman and Co. ISBN 0-7167-4361-2 . OCLC 53160439 .
- ^ David E. Joyce (1997). "Euclid's elements, Book 1, Proposition 20" . Euclid's elements . Dept. Math and Computer Science, Clark University . Diakses tanggal 2010-06-25 .
|
Artikel bertopik matematika ini adalah sebuah rintisan . Anda dapat membantu Wikipedia dengan . |