|
Artikel ini membutuhkan
rujukan tambahan
agar kualitasnya
dapat
dipastikan
.
(
Juni 2009
)
|
|
Struktur aljabar
→
Teori grup
Teori grup |
|---|

|
Di teori grup , cabang matematika , diberi grup G di bawah operasi biner ∗, himpunan bagian H dari G disebut subgrup dari G jika H juga membentuk grup di bawah operasi ∗. Lebih tepatnya, H adalah subgrup dari G jika restriksi dari ∗ ke H × H adalah operasi grup di H . Ini biasanya dilambangkan H ≤ G , dibaca sebagai " H adalah subgrup dari G ".
Coset dan teorema Lagrange
Diberikan subgrup H dan beberapa a di G, kita mendefinisikan kiri coset aH = { ah : h in H }. Karena a bisa dibalik, peta φ : H → aH diberikan pada φ( h ) = ah adalah bijeksi . Lebih jauh, setiap elemen G terkandung tepat di satu koset kiri H ; koset kiri adalah kelas kesetaraan yang sesuai dengan relasi ekivalen a 1 ~ a 2 jika dan hanya jika a 1 −1 a 2 ada di H . Jumlah koset kiri H disebut dari H dalam G dan dilambangkan dengan [ G : H ].
Teorema Lagrange menyatakan bahwa untuk grup berhingga G dan subgrup H ,
dimana | G | dan | H | menunjukkan dari G dan H , masing-masing. Secara khusus, urutan setiap subkelompok G (dan urutan setiap elemen G ) harus berupa pembagi dari | G |. [ 1 ] [ 2 ]
Contoh: Subgrup Z 8
Maka G jadikan grup siklik ke Z 8 maka hasil elemen
dan yang operasi grupnya adalah penambahan modulo delapan . adalah
| + | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 2 | 2 | 4 | 6 | 0 | 3 | 5 | 7 | 1 |
| 4 | 4 | 6 | 0 | 2 | 5 | 7 | 1 | 3 |
| 6 | 6 | 0 | 2 | 4 | 7 | 1 | 3 | 5 |
| 1 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0 |
| 3 | 3 | 5 | 7 | 1 | 4 | 6 | 0 | 2 |
| 5 | 5 | 7 | 1 | 3 | 6 | 0 | 2 | 4 |
| 7 | 7 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
Grup ini memiliki dua subgrup nontrivial: J ={0,4} and H ={0,2,4,6} , dimana J juga merupakan subgrup dari H . Tabel Cayley untuk H adalah kuadran kiri atas tabel Cayley untuk G . Grup G adalah siklik , dan juga subgrupnya.
Contoh: Subgrup S 4 ( grup simetris pada 4 elemen)
Setiap grup memiliki subgrup kecil sebanyak elemen netral pada diagonal utama:
The trivial group and two-element groups Z 2 . These small subgroups are not counted in the following list.

|
12 elements

Subgroups:





8 elements

Subgroups: 


|

Subgroups: 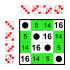

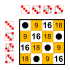
|

Subgroups: 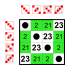


|
6 elements

Subgroup: 
|

Subgroup: 
|

Subgroup: 
|

Subgroup: 
|
4 elements

|

|

|

|

|

|

|
3 elements

|

|

|

|
Lihat pula
Catatan
- ^ Melihat sebuah didactic proof in this video .
- ^ S., Dummit, David (2004). Abstract algebra . Foote, Richard M., 1950- (edisi ke-3.). Hoboken, NJ: Wiley. hlm. 90. ISBN 9780471452348 . OCLC 248917264 .
Referensi
- (2009), Basic algebra , 1 (edisi ke-2nd), Dover, ISBN 978-0-486-47189-1 .
- (1974), Algebra (edisi ke-1st), Springer-Verlag, ISBN 9780387905181 .
- Artin, Michael (2011), Algebra (edisi ke-2nd), Prentice Hall, ISBN 9780132413770 .
- S., Dummit, David (2004). Abstract algebra . Foote, Richard M., 1950- (edisi ke-3.). Hoboken, NJ: Wiley. ISBN 9780471452348 . OCLC 248917264 .



















![{\displaystyle [G:H]={|G| \over |H|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e64b76d0605e6c7891273e65da28b5e431d4ea4)


