Ensiklopedia

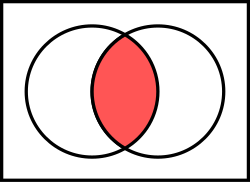
Dalam matematika, irisan dari dua himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ adalah himpunan yang memuat semua anggota dari ${\displaystyle A}$ juga milik ${\displaystyle B}$ (atau, semua anggota dari ${\displaystyle B}$ yang juga milik ${\displaystyle A}$ ). ^{[ 1 ]} Irisan dari kedua himpunan tersebut dinyatakan secara matematis: ^{[ 2 ] [ 3 ]}

${\displaystyle A\cap B}$ ,

Irisan ditulis menggunakan simbol "∩" di antara ekspresi berupa kumpulan anggota-anggota, dalam . Berikut adalah contoh-contohnya:

${\displaystyle \{1,2,3\}\cap \{2,3,4\}=\{2,3\}}$

${\displaystyle \{1,2,3\}\cap \{1,5,10\}\cap \{1,4,9\}=\{1\}}$

${\displaystyle \{1,2,3\}\cap \{4,5,6\}=\emptyset }$

${\displaystyle \mathbb {Z} \cap \mathbb {N} =\mathbb {N} }$

${\displaystyle \{x\in \mathbb {R} :x^{2}=1\}\cap \mathbb {N} =\{1\}}$

Ketika irisan terjadi lebih dari dua himpunan (irisan yang diperumum), notasinya mirip seperti notasi Sigma , yang ditulis sebagai

${\displaystyle \bigcap _{i=1}^{n}A_{i}}$ .

Irisan dari huruf Yunani , Latin , dan Rusia , hanya dipandang sebagai bentuk-bentuk dari huruf-huruf dan mengabaikan pengucapannya.

Contoh irisan dari himpunan.

Irisan dari dua himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ , dilambangkan dengan ${\displaystyle A\cap B}$ , ^{[ 2 ] [ 4 ]} merupakan himpunan dari semua objek yang merupakan anggota dari kedua himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ . Secara matematis, ditulis

${\displaystyle A\cap B=\{x:x\in A{\text{ dan }}x\in B\}.}$

Hal ini mengartikan bahwa ${\displaystyle x}$ adalah anggota dari irisan ${\displaystyle A\cap B}$ jika dan hanya jika ${\displaystyle x}$ adalah anggota dari ${\displaystyle A}$ dan anggota dari ${\displaystyle B}$ . ^{[ 4 ]} Sebagai contohː

• Irisan dari himpunan ${\displaystyle \{1,2,3\}}$ dan ${\displaystyle \{2,3,4\}}$ adalah ${\displaystyle \{2,3\}}$ .
• Bilangan 9 bukanlah irisan dari himpunan bilangan prima ${\displaystyle \{2,3,5,7,11,\dots \}}$ dan himpunan bilangan ganjil ${\displaystyle \{1,3,5,7,9,11,\dots \}}$ , karena 9 bukanlah bilangan prima.

Himpunan ${\displaystyle A}$ dikatakan beririsan dengan himpunan ${\displaystyle B}$ jika terdapat ${\displaystyle x}$ yang merupakan anggota dari himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ .

Himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ dikatakan saling lepas jika ${\displaystyle A}$ tidak beririsan dengan ${\displaystyle B}$ . Penjelasan yang lebih sederhananya, kedua himpunan tersebut tidak memiliki anggota yang sama. Himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ saling lepas jika irisannya adalah kosong , dilambangkan ${\displaystyle A\cap B=\varnothing }$ .

Sebagai contoh, himpunan ${\displaystyle \{1,2\}}$ dan ${\displaystyle \{3,4\}}$ saling lepas, sedangkan himpunan bilangan genap beririsan dengan himpunan kelipatan dari 3 di himpunan kelipatan 6.

• Irisan adalah operasi yang bersifat komutatif ; yaitu, untuk setiap himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ , berlaku:
  ${\displaystyle A\cap B=B\cap A}$ .
• Irisan adalah operasi yang bersifat asosiatif ; yaitu, untuk setiap himpunan ${\displaystyle A}$ , ${\displaystyle B}$ , dan ${\displaystyle C}$ , berlaku:
  ${\displaystyle A\cap (B\cap C)=(A\cap B)\cap C}$ .
  Berdasarkan sifat ini, penulisan lambang kurung boleh diabaikan sama sekali tanpa mengubah makna; sehingga bentuk di atas dapat ditulis sebagai ${\displaystyle A\cap B\cap C}$ .
• Irisan bersifat idempoten; yakni, untuk sebarang himpunan ${\displaystyle A}$ berlaku
  ${\displaystyle A\cap A=A}$

Sifat-sifat tersebut bersesuaian dengan logika konjungsi

• Irisan bersifat distributif terhadap gabungan dan gabungan bersifat distributif terhadap irisan; yaitu, untuk setiap himpunan ${\displaystyle A}$ dan ${\displaystyle B}$ , berlaku:
  ${\displaystyle A\cup (B\cap C)=(A\cup B)\cap (A\cup C)}$ .
  ${\displaystyle A\cap (B\cup C)=(A\cap B)\cup (A\cap C)}$ .
• Dalam semesta ${\displaystyle U}$ , komplemen ${\displaystyle A^{\complement }}$ dari himpunan ${\displaystyle A}$ dapat didefinisikan sebagai himpunan dari semua anggota dari ${\displaystyle U}$ yang tidak termuat dalam ${\displaystyle A}$ . Selanjutnya, irisan dari ${\displaystyle A}$ dan ${\displaystyle B}$ dapat ditulis sebagai komplemen dari gabungan dari komplemennya, diturunkan dengan mudah dari ː $${\displaystyle A\cap B=\left(A^{c}\cup B^{c}\right)^{c}.}$$

Perumuman gagasan irisan adalah irisan sebarang kumpulan takkosong himpunan-himpunan. Jika ${\displaystyle M}$ adalah himpunan bukan kosong yang anggotanya adalah himpunan juga, maka ${\displaystyle x}$ adalah anggota dari irisan dari ${\displaystyle M}$ jika dan hanya jika untuk setiap anggota ${\displaystyle A}$ dari ${\displaystyle M}$ , ${\displaystyle x}$ adalah sebuah anggota dari ${\displaystyle A}$ . Secara matematis ditulisː

${\displaystyle \left(x\in \bigcap _{A\in M}A\right)\Leftrightarrow \left(\forall A\in M,\ x\in A\right)}$ .

Notasi mengenai konsep terakhir ini dapat ditulis dengan berbagai cara. Sebagian pakar teori himpunan terkadang menulis ${\textstyle \bigcap M}$ , sementara yang lainnya menulis ${\textstyle \bigcap _{A\in M}A}$ . Penulisan notasi terakhir dapat diperumum menjadi ${\textstyle \bigcap _{i\in I}A_{i}}$ , yang mengacu pada irisan kumpulan ${\displaystyle \{A_{i}:i\in I\}}$ . Dalam notasi terakhir itu, ${\displaystyle I}$ adalah himpunan takkosong, dan ${\displaystyle A_{i}}$ adalah sebuah himpunan dari setiap ${\displaystyle i}$ dalam ${\displaystyle I}$ .

Pada sebuah kasus bahwa himpunan indeks ${\displaystyle I}$ adalah himpunan bilangan asli , notasi irisan sembarang mirip dengan notasi .

${\displaystyle \bigcap _{i=1}^{\infty }A_{i}}$ .

Notasi tersebut juga dapat ditulis ${\displaystyle A_{1}\cap A_{2}\cap A_{3}\cap \dots }$ .

Perhatikan bahwa dalam bagian sebelumnya, kita mengecualikan kasus untuk ${\displaystyle M}$ adalah himpunan kosong ( ${\displaystyle \varnothing }$ ). Alasannya adalah bahwa Irisan dari kumpulan ${\displaystyle M}$ didefinisikan sebagai himpunan (lihat notasi ungkapan himpunan )

${\displaystyle \bigcap _{A\in M}A=\{x:\forall A\in M,x\in A\}.}$

Jika ${\displaystyle M}$ kosong, maka tidak ada himpunan ${\displaystyle A}$ dalam ${\displaystyle M}$ . Hal ini memunculkan sebuah pertanyaan: " ${\displaystyle x}$ manakah yang memenuhi syarat yang disebutkan?". Jawabannya bisa saja untuk setiap kemungkinan ${\displaystyle x}$ . Ketika ${\displaystyle M}$ kosong, syarat yang disebutkan di atas merupakan sebuah contoh dari . Jadi, irisan dari keluarga kosong harus berupa himpunan semesta ( anggota identitas untuk operasi dari irisan), ^{[ 5 ]} namun dalam teori himpunan ( ) standar, himpunan semesta tidak ada.

• Aljabar himpunan
• Beda setangkup
• Gabungan
• Kardinalitas
• Komplemen
• Logika konjungsi
• Operasi biner teriterasi

1. ^ "Stats: Probability Rules" . People.richland.edu . Diakses tanggal 2012-05-08 .
2. ^ ^{a b} "Comprehensive List of Set Theory Symbols" . Math Vault (dalam bahasa Inggris). 2020-04-11 . Diakses tanggal 2020-09-04 .
3. ^ "Intersection of Sets" . web.mnstate.edu . Diarsipkan dari versi asli tanggal 2020-08-04 . Diakses tanggal 2020-09-04 .
4. ^ ^{a b} "Set Operations | Union | Intersection | Complement | Difference | Mutually Exclusive | Partitions | De Morgan's Law | Distributive Law | Cartesian Product" . www.probabilitycourse.com . Diakses tanggal 2020-09-04 .
5. ^ (1998), "Chapter 1", An introduction to Banach space theory , , 183 , New York: Springer-Verlag, hlm. xx+596, ISBN 0-387-98431-3

• (1993). The Joy of Sets: Fundamentals of Contemporary Set Theory (edisi ke-Second). New York, NY: Springer-Verlag. ISBN 3-540-94094-4 .
• (2000). "Set Theory and Logic". Topology (edisi ke-Second). Upper Saddle River: Prentice Hall. ISBN 0-13-181629-2 .
• Rosen, Kenneth (2007). "Basic Structures: Sets, Functions, Sequences, and Sums". Discrete Mathematics and Its Applications (edisi ke-Sixth). Boston: McGraw-Hill. ISBN 978-0-07-322972-0 .

• Weisstein, Eric W. "Intersection". MathWorld.